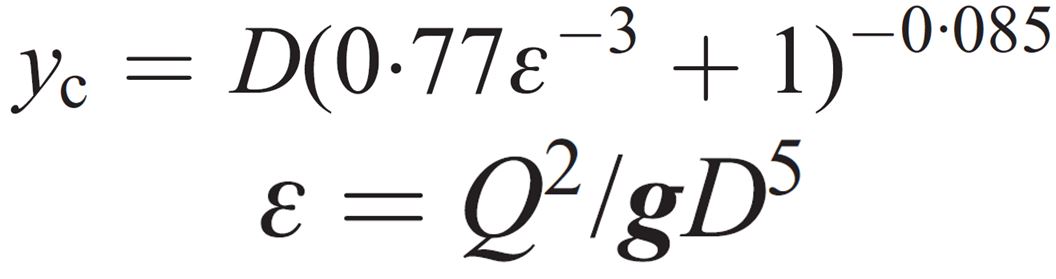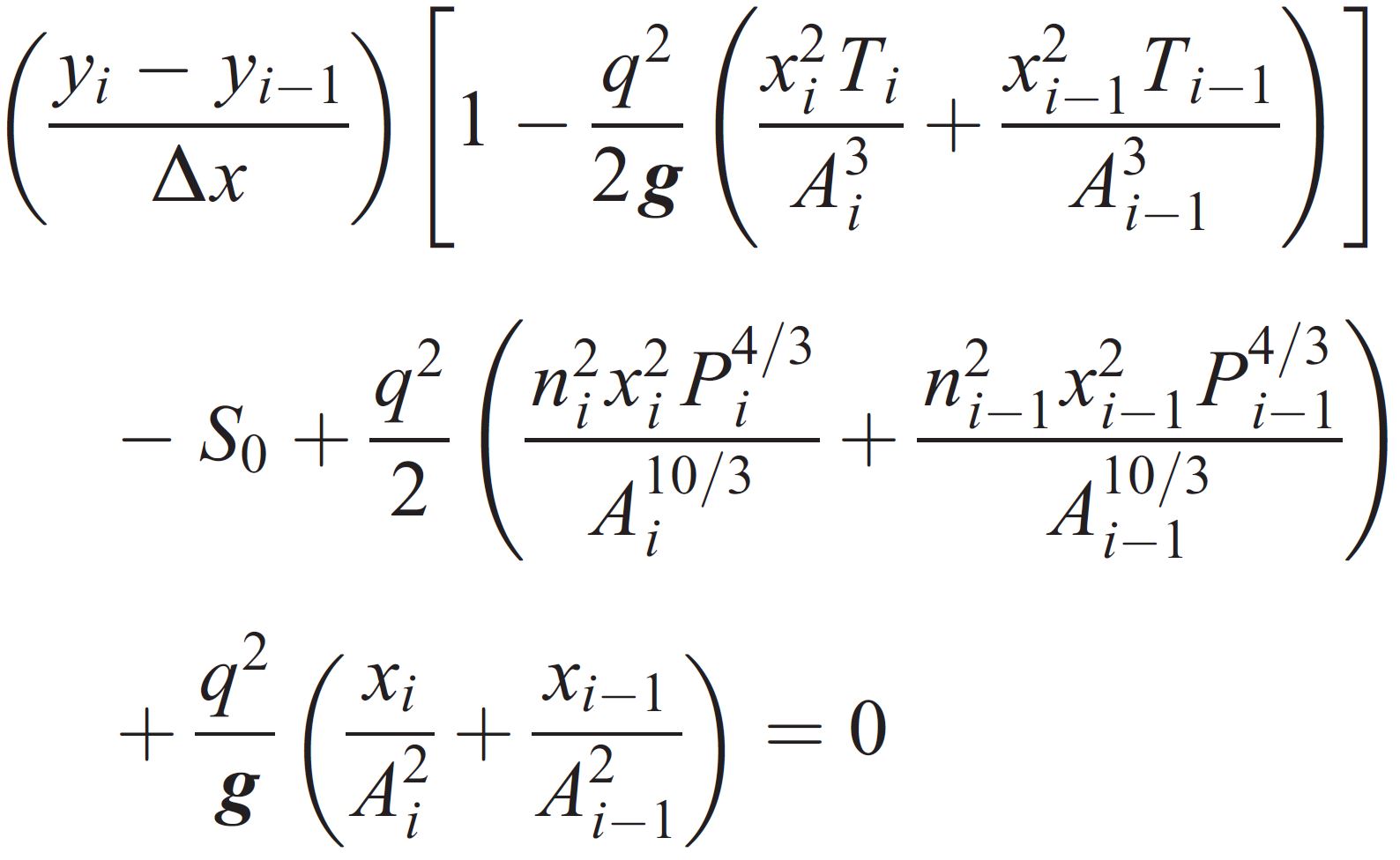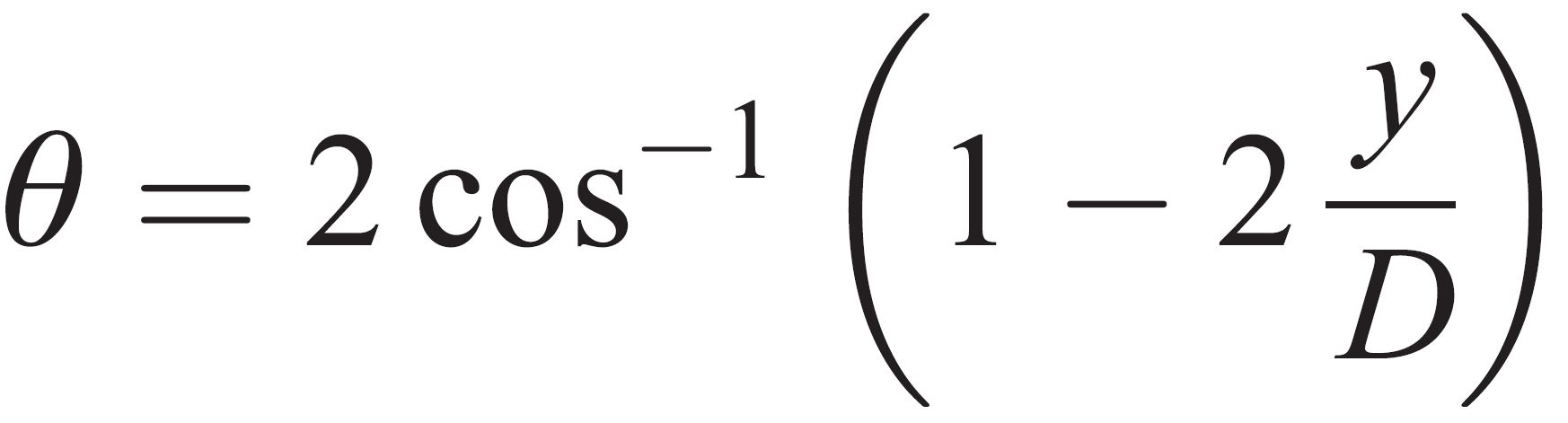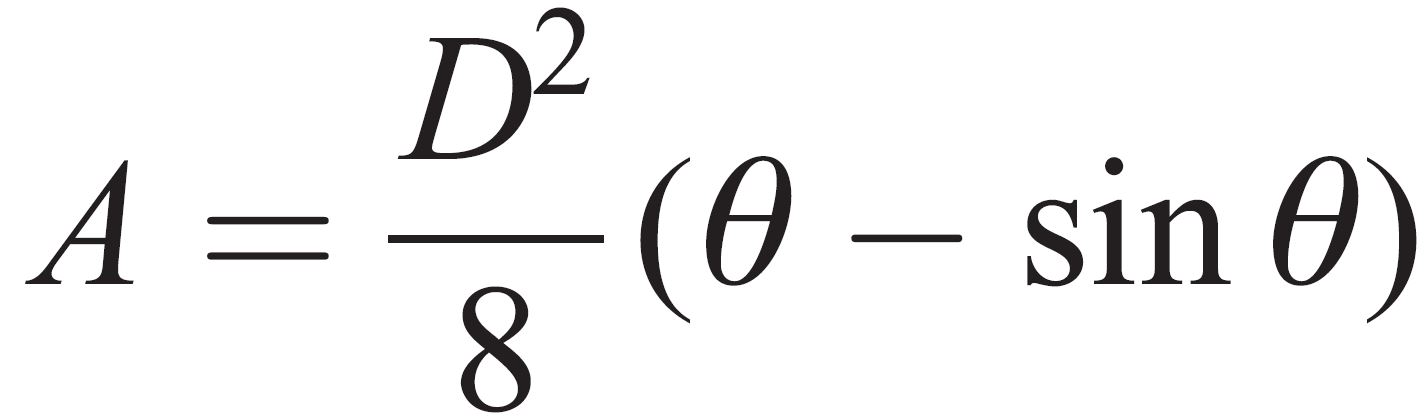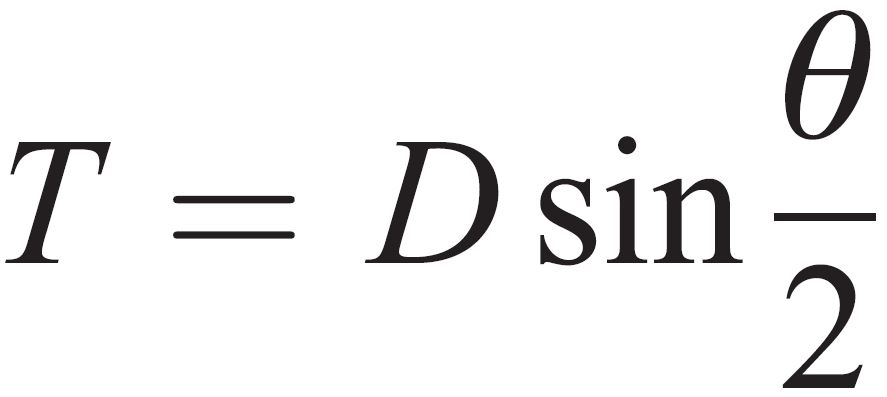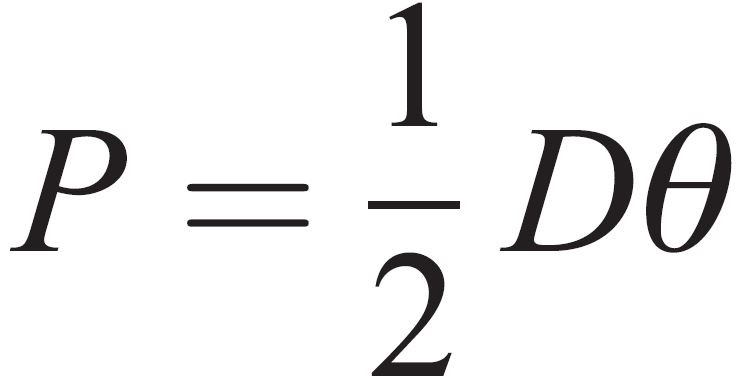French drains can be modelled as a spatially varied flow system as they accept runoff in a reasonably consistent rate along the whole length of the french drain. Traditionally the perforated pipe design for french drain systems is completed in the same way as the design of non-perforated drainage pipes which accept all their water at the head of the run and usually do not accept any further flow until the end of that discrete run. French drains however usually have no flow at the head of the run but accept inflow along the entire length of the run.
This french drain system can be more accurately modelled as a spatially varied flow model. The CivilWeb French Drain Design spreadsheet includes a special spreadsheet tool which models the perforated pipe as a spatially varied flow model giving the designer a more accurate picture of how the flow will change along the french drain and the required pipe size to accommodate this flow.
Spatially Varied Flow Analysis
It is general practice to design the french drain in the same way as a conventional drainage pipe using either the Colebrook-White Equation or Manning’s Equation for circular cross section pipes. These formula are used to determine the maximum discharge of the proposed pipe. The total inflow into the french drain is then compared with the maximum discharge to determine whether the proposed pipe and gradient is suitable. This process is described in more detail in our Perforated Pipe Design post.
In most practical situations a french drain can be considered as a spatially varied flow as the inflow to the pipe is fairly constant along the length of the pipe. This increases the discharge as the pipe flows from upstream to downstream end. This differs from a typical drainage pipe where the inflow mostly occurs at the upstream end of the pipe. The CivilWeb French Drain Design Spreadsheet includes a unique design tool which analyses the proposed french drain using a complex finite difference model of spatially varied flow analysis. The spreadsheet presents a graph showing the water level throughout the length of the pipe which can be used to determine whether the proposed french drain pipe is adequate.
Critical Depth
In order to complete the finite difference analysis of the spatially varied flow within the pipe, there must be a point at which the flow depth is known. This known point is required as a starting point for the finite difference analysis which then works backwards up the pipe from this known point. One point which can be calculated directly is the critical depth.
When designed correctly and under normal conditions french drains will flow with a free water surface within the pipe and the flow is subcritical for the whole length. When the outfall from the pipe is free and the flow is subcritical the critical depth (yc) will occur at the outfall of the pipe. Assuming this is the case, the critical depth can be calculated from the following equations;
Pipe Diameter (D)
This is the internal diameter of the perforated pipe being analysed.
Dimensionless Discharge Coefficient (ε)
This dimensionless coefficient describes the relationship between the flow through the pipe and its diameter. It is calculated using the above equation which is then plugged into the critical depth equation.
Total Flow at Outfall (Q)
The total flow at the outfall is equal to the entire inflow into the pipe. This is determined by multiplying the inflow rate (q) by the length of the pipe.
Acceleration due to Gravity (g)
The acceleration due to gravity is typically taken as 9.81m/s2.
Finite Difference Analysis
Assuming that this critical depth occurs at the outfall of the pipe, this known value and location can be used as a starting point for the finite difference analysis. The flow conditions in a pipe subject to spatially varied flow at a point close to a known value can be determined from the below finite difference equation;
Water Flow Depth (y)
This is the water flow depth at a known point (yi) and at a point just upstream (yi-1). This value is the desired result of the equation but cannot be obtained directly as many of the other parameters such as area of flow, wetted perimeter and flow width all depend on the flow depth. The CivilWeb French Drain Design spreadsheet is able to estimate this value using an iterative computational technique.
Distance from the Upstream End of Pipe (x)
This is the distance of the known point (xi) and the point being analyzed (xi-1) from the upstream end of the pipe. The computational step distance (Δx) is also required in the equation. The CivilWeb French Drain Design Spreadsheet breaks the pipe length into 1,000 pieces for the analysis in order to minimize the inaccuracies inherent in the method. The finite difference analysis method works better with small slices so care should be taken when analyzing pipes longer than around 500m.
Inflow Rate into Pipe (q)
This is the inflow rate into the pipe per length of pipe. This is determined through a rainfall analysis.
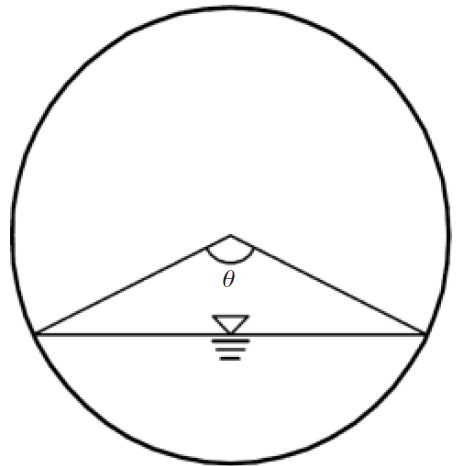
Water Surface Angle (θ)
This is the geometrical angle of the water flow within the pipe as shown in the below diagram. This parameter is not directly included in the above equation but is required in order to calculate the flow area, wetted perimeter and water flow width. It can be calculated from the flow depth (y) and pipe diameter (D) using the below equation.
Cross Sectional Area of Flow (A)
This is the area of the flow through the pipe at a known point (Ai) and at the point being considered (Ai-1). This can be calculated from the water flow angle (θ) and the pipe diameter (D) using the below equation;
Flow Width (T)
This is the width of the free surface of the water as it flows through the pipe at a known point (Ti) and at the point being analyzed (Ti-1). This can be calculated from the water flow angle (θ) and the pipe diameter (D) using the below equation;
Wetted Perimeter (P)
This is the internal length of the pipe which is in contact with the water flow at a known point (Pi) and at the point being analyzed (Pi-1). This is used to take account of the energy lost through friction between the water and the pipe. This can be calculated from the water flow angle (θ) and the pipe diameter (D) using the below equation;
Manning Coefficient (n)
The Manning Coefficient is used to account for the different amounts of energy lost to friction with different pipe materials and conditions. The equation above allows for two different values to be used if the Manning Coefficient is expected to change over the length of the pipe. In most cases it is reasonable to model the Manning Coefficient as unchanging.
Hydraulic Slope of Pipe (S0)
This is the slope or gradient of the pipe running from upstream to downstream end. French drains are typically laid a very shallow gradients of 1 in 100 or shallower. For french drains laid at steep gradients the designer should check that the flow will be subcritical for the whole length of pipe.
CivilWeb French Drain Design Spreadsheet – Spatially Varied Flow Analysis
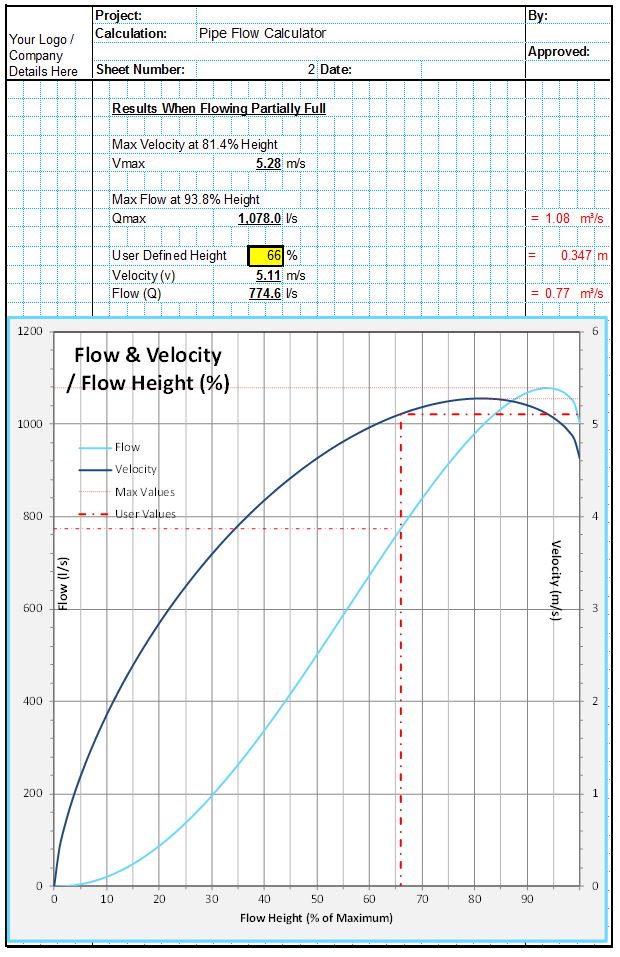
The CivilWeb French Drain Design spreadsheet completes the complex finite difference analysis of the french drain as a spatially varied flow system. It does this for 1,000 separate sections along the pipe in order for the finite difference analysis to work accurately. It then displays the results in a graph showing the flow depth at all sections of the pipe from upstream end to outfall and presents the highest calculated flow height. If this is less than the overall diameter of the pipe then the pipe is suitable. If the pipe is not suitable the analysis will typically break down and return an error. In this case the designer should present a larger diameter pipe or a steeper slope and run the analysis again until a satisfactory result is achieved.
Get your copy of the CivilWeb French Drain Design spreadsheet now for only £20.
Or why not bundle with the CivilWeb Soakaway Design spreadsheet for only £5 extra?
Or save £50 by buying our full Drainage Design Suite including all our drainage design spreadsheets.
Download Free Trial Version
To try out a fully functional free trial version of this software, please Click Here or enter your email address below to sign up to our newsletter.