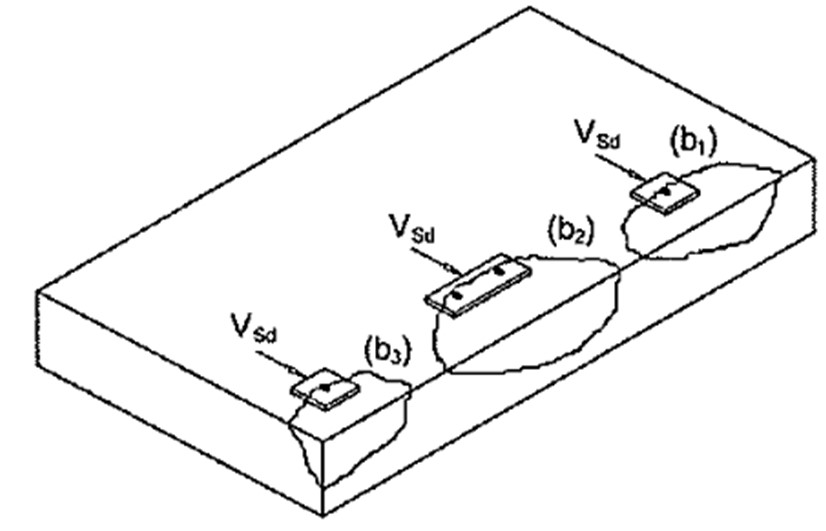
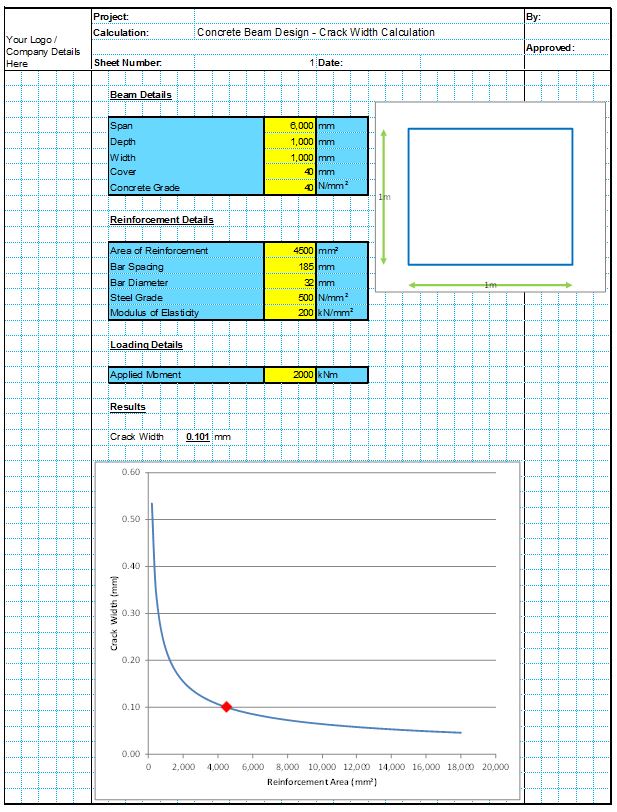
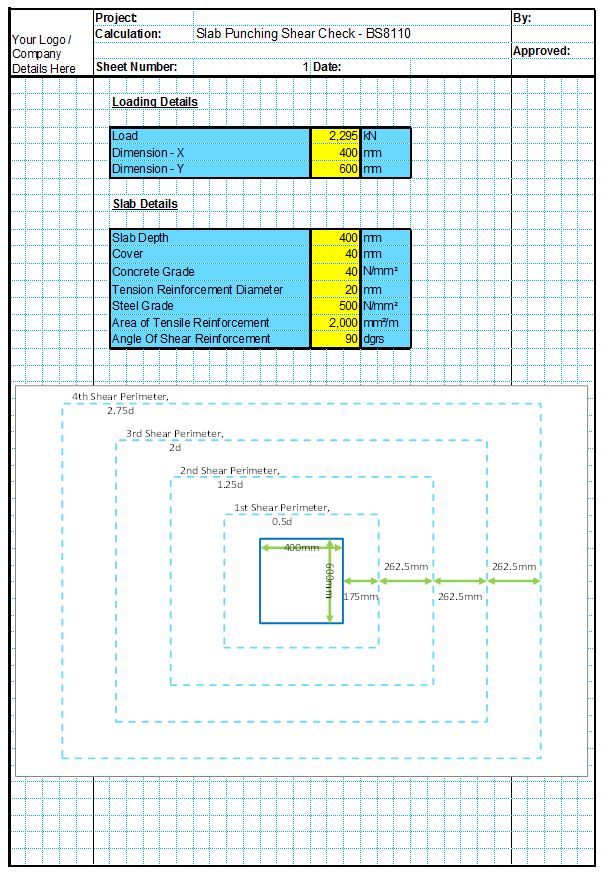
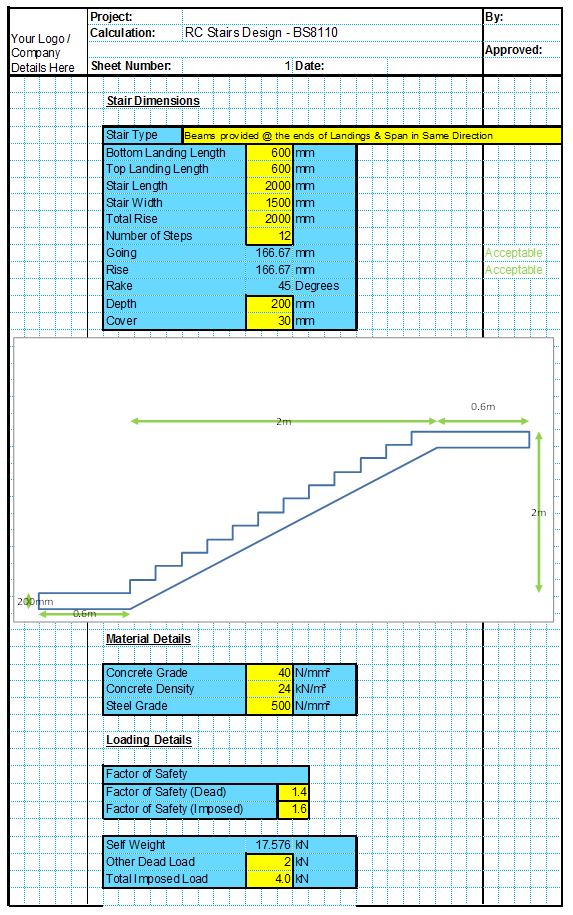
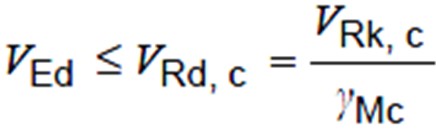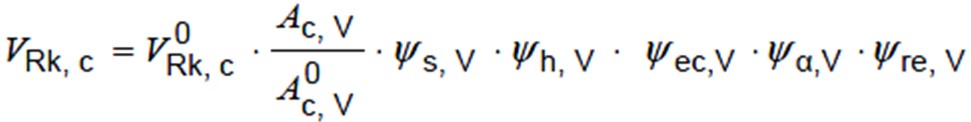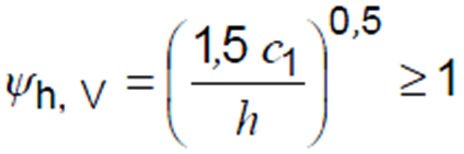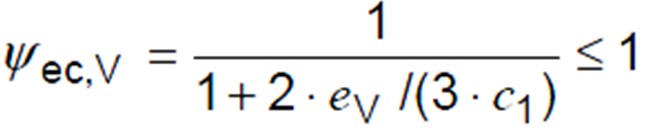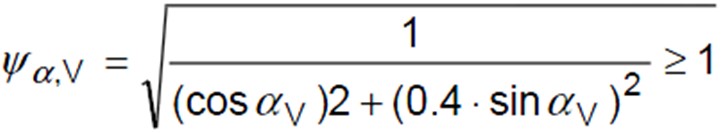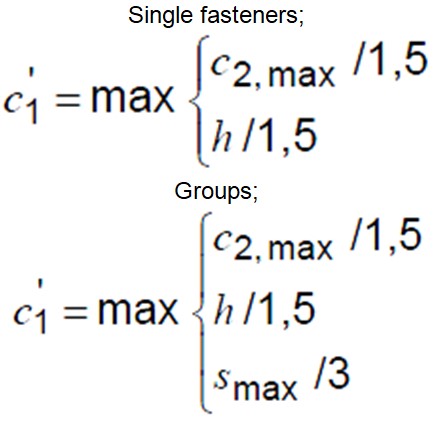Concrete Edge Failure can occur when the concrete fails towards an edge under shear loading, as shown in the below diagrams. This mode of failure can occur for cast in anchors, mechanical anchors or chemical anchors. The CivilWeb Concrete Anchorage Design Spreadsheet completes all the concrete edge failure calculations detailed below for cast in anchors, mechanical anchors and chemically bonded anchors in accordance with BS EN 1992-4.
Concrete Edge Failure Design Checks Required
For single anchors or groups with 4 or less bolts, an edge resistance design check is not required if the following equations are satisfied;
Distance to all Edges (c)
Effective Depth (hef)
This is the effective depth of the anchor.
Diameter of the Bolt (d)
This can be taken from the manufacturer’s info.
Concrete Edge Failure Design Checks
Where design checks are required this should be done for all suitable edges, as shown in the below diagram.
To avoid concrete edge failure the Design Concrete Edge Failure Resistance (VRd, c) must be greater than or equal to the Design Shear Force (VEd), as shown in the below equation.
Partial Safety Factor for Concrete Splitting Failure (γMc)
This is the partial factor of safety applied to concrete failure. A value of 1.5 is typically recommended.
Characteristic Concrete Edge Failure Resistance (VRk, c)
This can be calculated using the following equations;
Initial Characteristic Concrete Edge Failure Resistance (VRk0, c)
The initial value can be calculated using the below equations;
Diameter of the Bolt (dnom)
This can be taken from the manufacturer’s info. This should not exceed 60mm.
lf
This can be taken from the manufacturer’s instructions. Otherwise this can be taken as the Effective Depth (hef). For this calculation this value should not exceed 8 times dnom.
Effective Depth (hef)
This is the effective depth of the anchor.
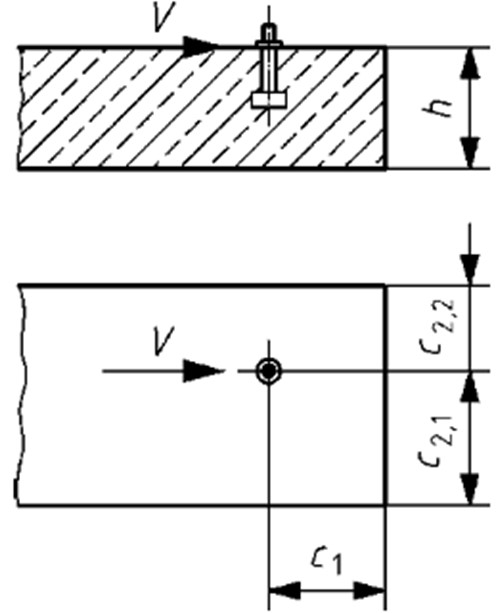
Edge Distance (C1)
This is the distance from the centre of the anchor to the edge in the direction of the shear load.
Characteristic Cube Strength of Concrete (fck,cube)
This can be taken from tests taken during the concrete pour or from design info. Manufacturer’s info should be checked to ensure that a limiting value is not specified.
Geometric Effects Factors (Ac,V & A0c,V)
The overall edge capacity of a fastener or group of fasteners is affected by the proximity of the concrete edges and by the effects of overlapping zones from adjacent fasteners.
Reference Projected Area (A0c,V)
This is the idealized projected area for a single fastener. This can be calculated with the following equation, illustrated with the below diagram;
Actual Projected Area (Ac,V)
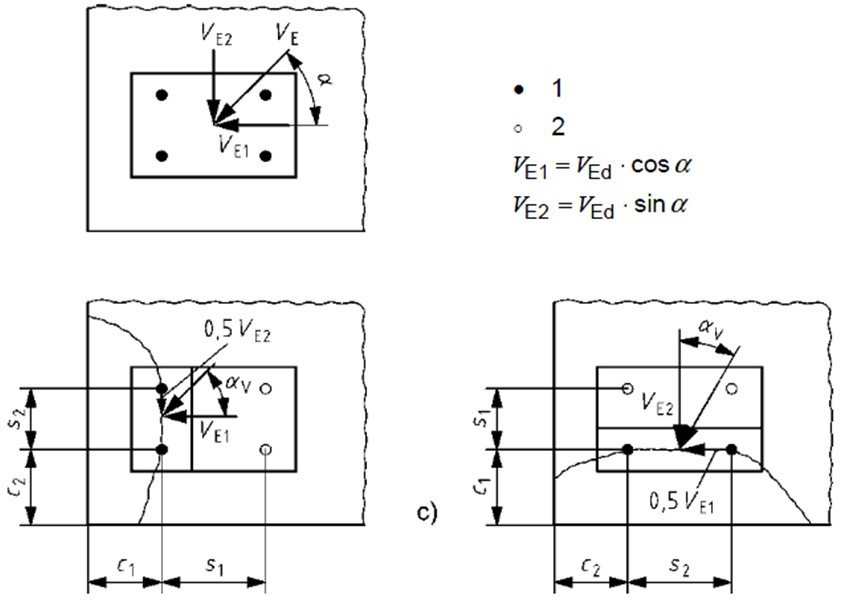
This is the actual projected area for the fastener or group including confinement by overlapping cones of adjacent fasteners in the same group and any additional edges parallel to the shear load. A few examples of this calculation are shown below;
Concrete Edge Effects Factor (Ψs,V)
When a fastener or group is placed close to the edge of the concrete unit this alters the distribution of stresses in the concrete. This effect can have a significant reduction in the concrete edge capacity when fasteners are installed close to the concrete edges. This effect can be calculated using the below equation;
Distance to Concrete Edges Other Than c1 (c2)
Member Thickness Effects Factor (Ψh, V)
This factor takes account of the effects of the member thickness. The resistance does not decrease proportionally to the thickness as assumed in the projected area values. This factor can be calculated using the below equation;
Depth of the Member (h)
Eccentricity Effects Factor (Ψec,V)
This factor takes account of the effects of eccentrically loaded anchor groups. This can be calculated using the below equation;
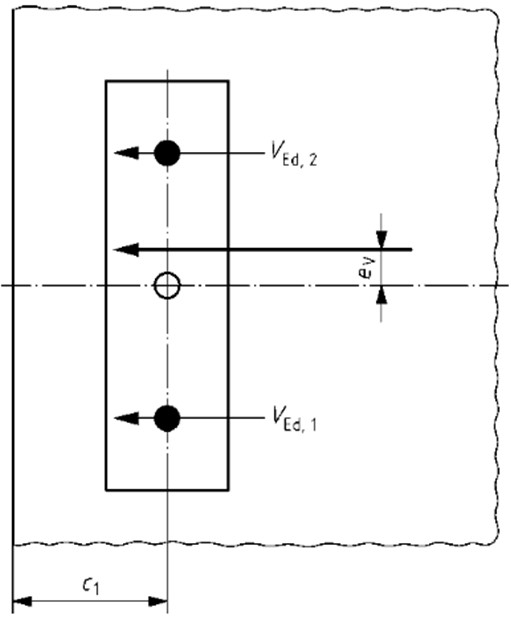
Eccentricity of the Resulting Shear Load (eV)
As shown in the below diagram;
Where the resulting tensile load is eccentric in two directions, the factor should be calculated in each direction and multiplied together.
Load Direction Effect Factor (Ψa,V)
This factor takes account of the angle between the load applied and the angle perpendicular to the edge considered. This can be calculated using the below equation;
Angle Between Load Applied and Perpendicular (a,V)
Cracked Concrete Factor (Ψre,V)
This factor takes account of whether the fastening is positioned in cracked or uncracked concrete. The following equations can be used to calculate this factor;
Values greater than 1.0 can only be applied in cracked concrete when the Effective Depth (hef) is greater than 2.5 times the concrete cover to the edge reinforcement.
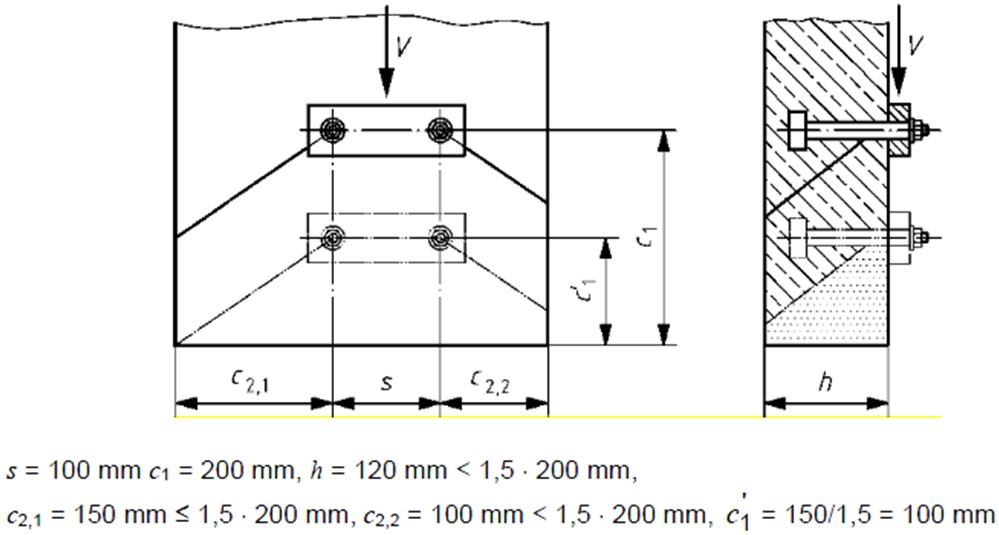
Narrow Thin Member Effects
For narrow thin members with c2,max and member depth less than 1.5 times c1 the above calculation is conservative. An example is shown below;
For more accurate results the c1 value can be limited using the below equations.
Largest of the Two Edge Distances Parallel to the Direction of Loading (c2,max)
Maximum Spacing Between Fasteners (smax)
An example is shown in the diagram below;
Concrete edge failure can be a critical design verification in cases where the anchor needs to be placed close to the edge of the concrete member. Obviously the best way to mitigate this effect is to move the anchor further away from the concrete edge but this is not always possible. The CivilWeb Concrete Anchorage Spreadsheet completes the calculations detailed above to check the concrete edge failure design case. It includes unique design tools including graphs which show the designer the sensitivity of the key design parameters at a glance.
Get your copy of the CivilWeb Concrete Anchorage Design Spreadsheet now for only £20.
Download Free Trial Version
To try out a fully functional free trail version of this software, please Click Here or enter your email address below to sign up to our newsletter.