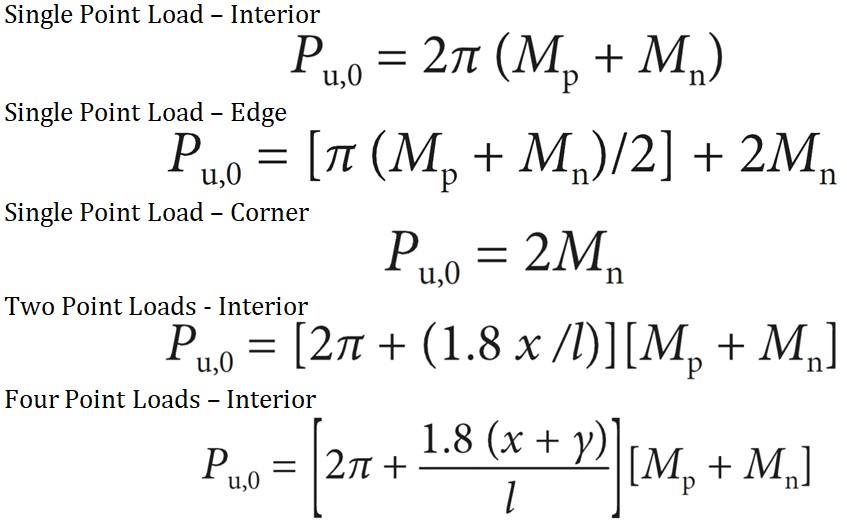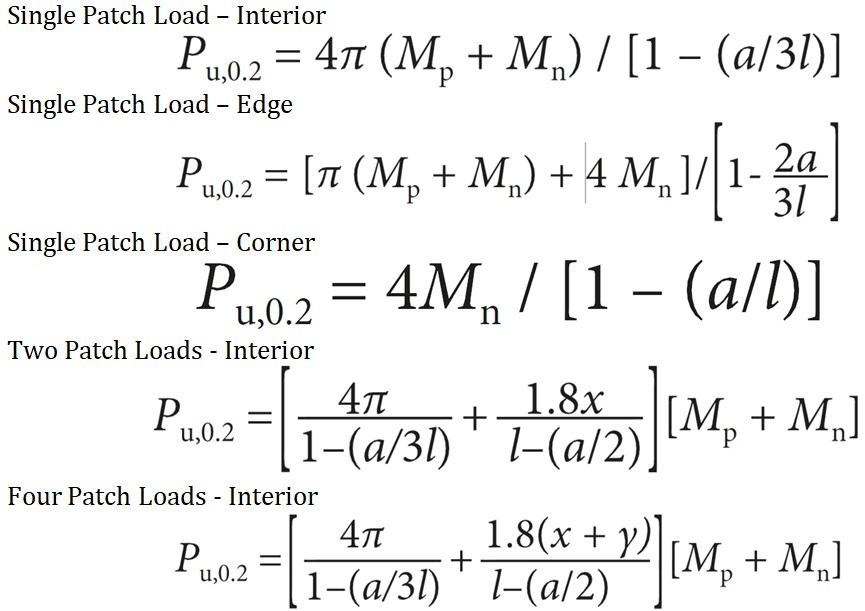Concrete Society Technical Report 34 Design Spreadsheet

Concrete Society Technical Report 34 includes a method of designing industrial concrete pavements. This is also often referred to as concrete society TR34 or even TR34 concrete pavement design.

The method included in Concrete Society Technical Report 34 follows Meyerhof's method of analysis and is well suited to the design of internal warehouse floors and similar where the critical loadings are from racking systems or mezzanine floors rather than from wheeled vehicles. The design method also assumes that some cracking in the floor is not critical.

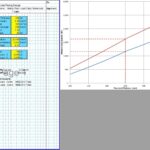
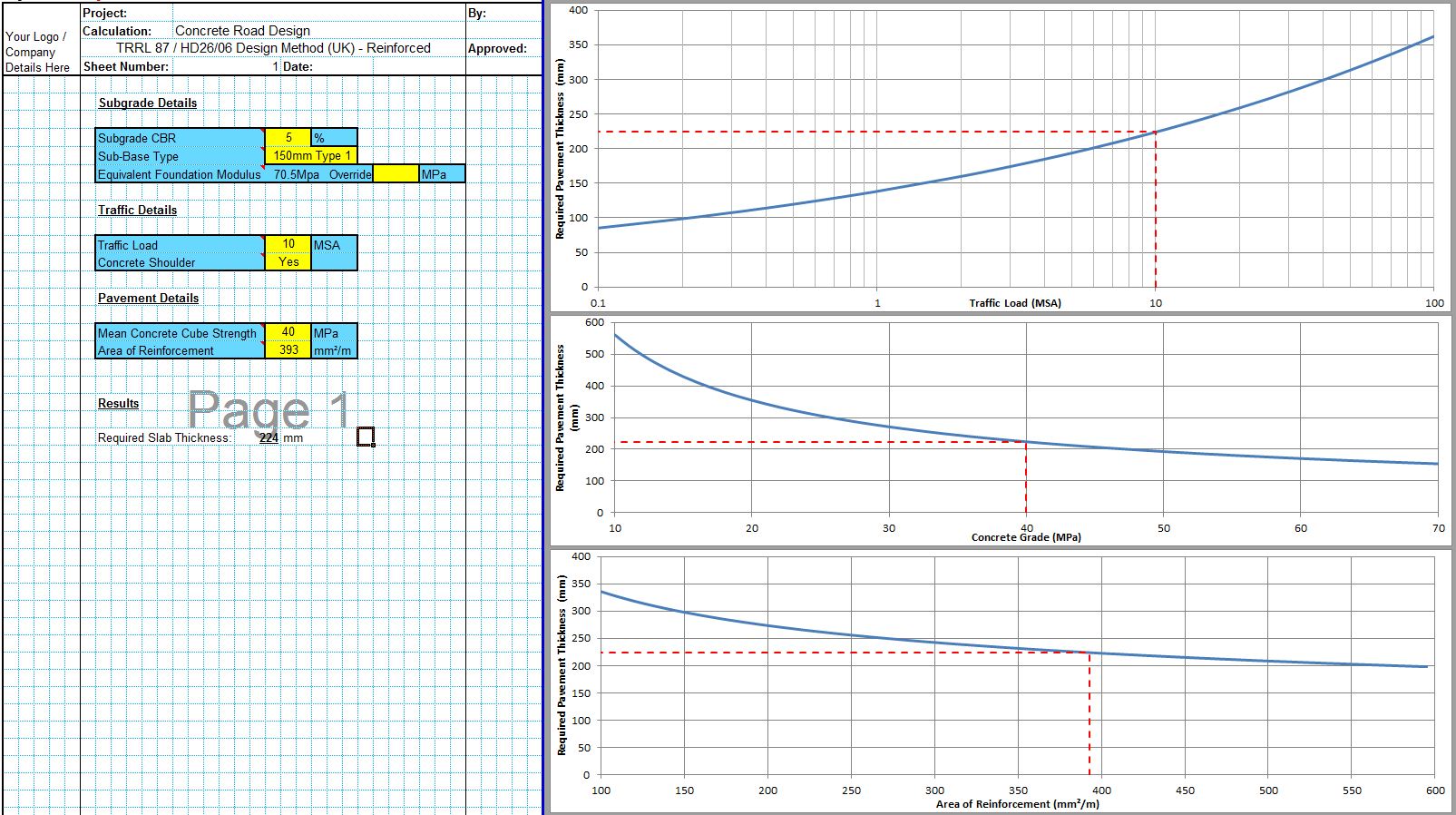
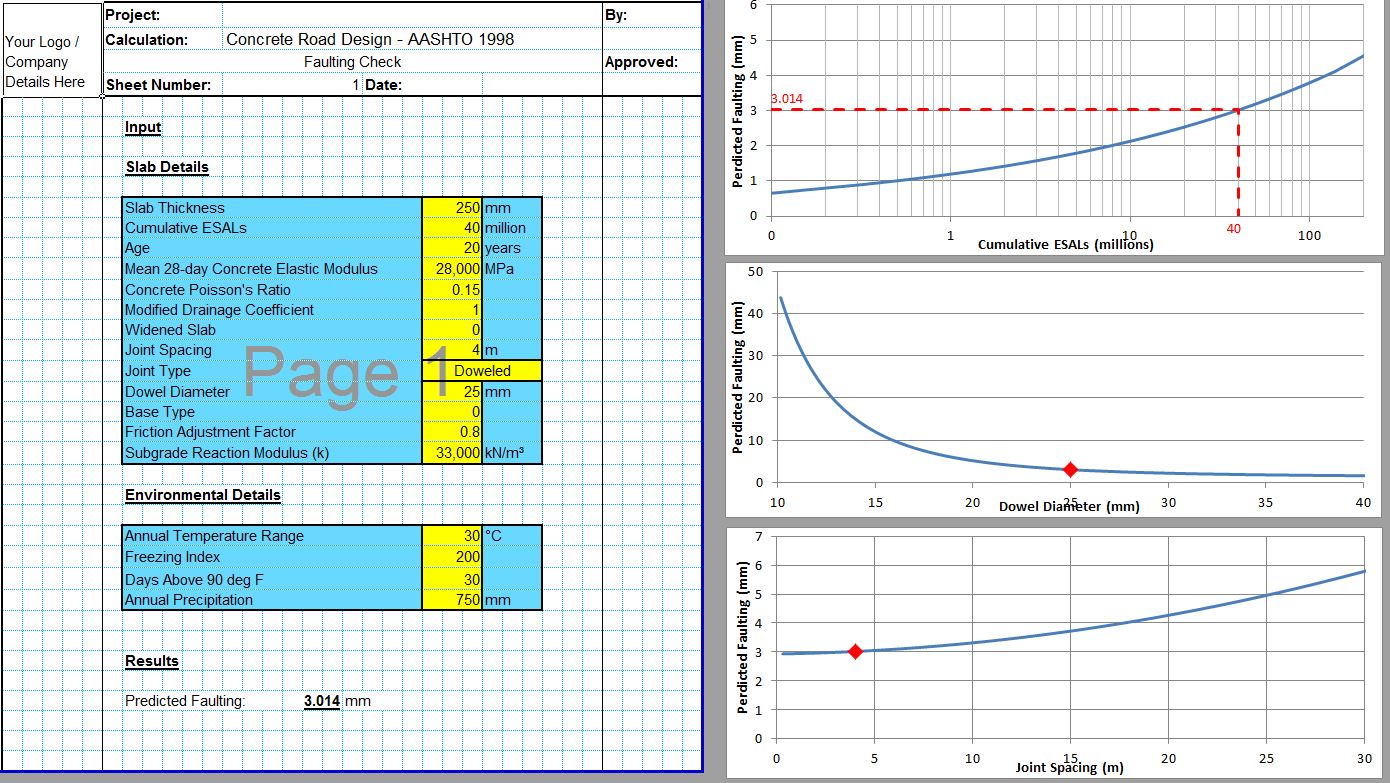
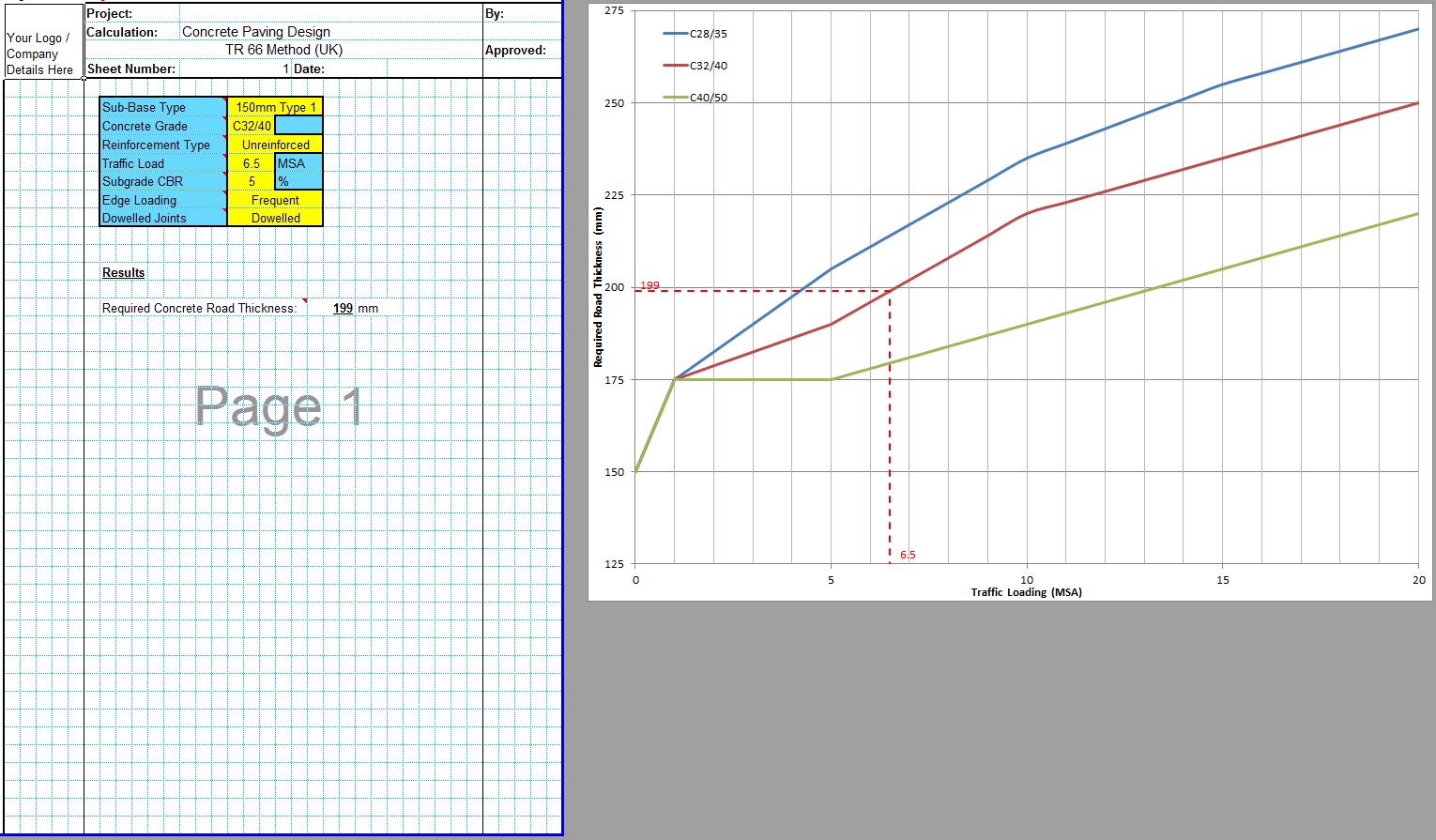
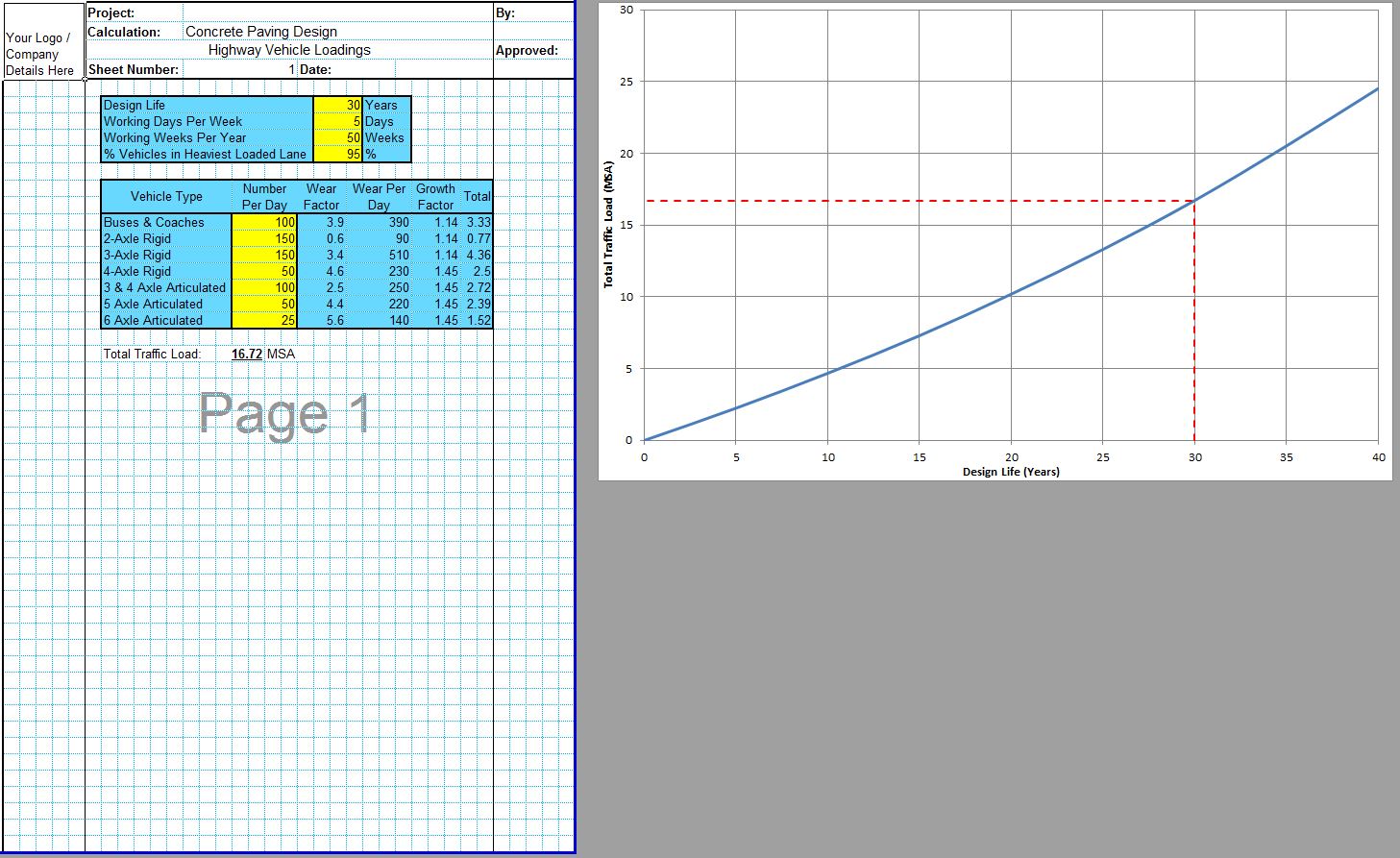
The CivilWeb Concrete Society Technical Report 34 Pavement Design Spreadsheet uses the methods described in Concrete Society Technical Report 34 to design internal concrete floors subjected to warehouse type loadings. The spreadsheet allows the designer to produce concrete pavement designs compliant with Concrete Society Technical Report 34 recommendations in seconds.

The CivilWeb Concrete Society Technical Report 34 Concrete Pavement Design Spreadsheet can be purchased further down this page for only £10. Alternatively the heavy duty concrete pavement design spreadsheet is included in the CivilWeb Rigid Pavement Design Suite which includes 11 different pavement design methods along with a number of other useful design tools including concrete flexural strength calculators. Follow the above link for full details.

Concrete Pavement Thickness Design – Meyerhof Method & TR 34

The Concrete Society Technical Report 34 method or Meyerhof method is a commonly used concrete pavement thickness design method, particularly for warehouse floors. The Concrete Society Technical Report 34 method is based on yield line analysis theory which allows some very simple equations to be used to determine the ultimate capacity of the slab for single and multiple point and patch loadings. The Concrete Society Technical Report 34 method can also be referred to as a limit state or plastic hinge analysis.

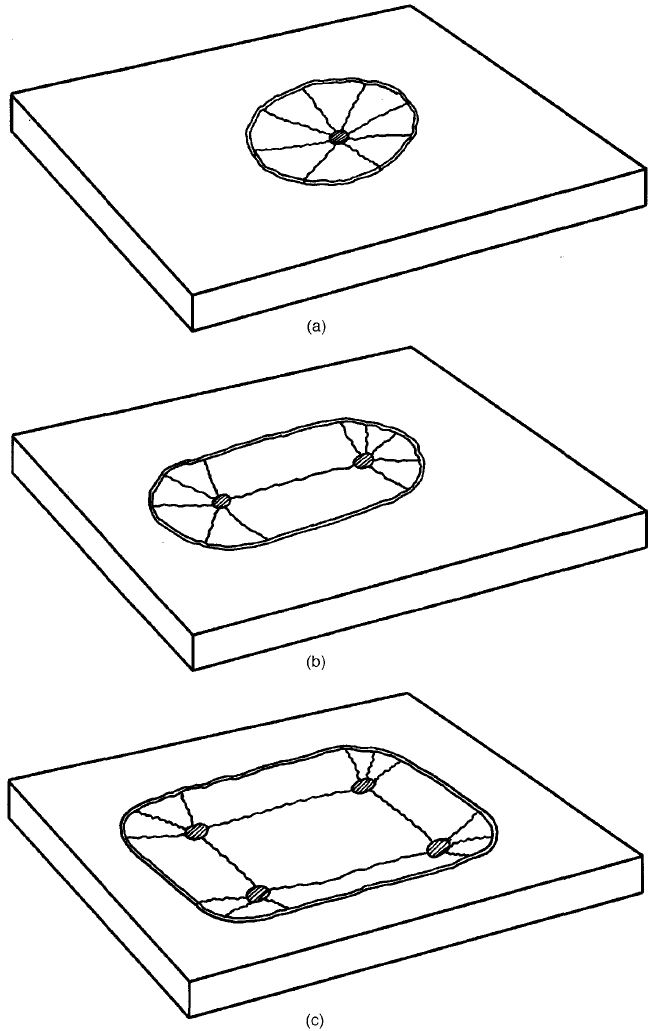
The Concrete Society Technical Report 34 method assumes that the concrete slab will fail in a particular manner. Meyerhof assumed that for the concrete slab to fail cracks would need to form in both the tensile zones at the top and the bottom of the slab. The failed slab would be transformed into a series of plates separated by plastic hinges or cracks in the concrete. The assumed failure modes for single, dual and multiple loads are shown below.

Concrete Society Technical Report 34- Modes of Failure Diagram

The failure of the slab would start as the failure of the section directly below the load in tension. This would cause the slab to yield or crack. This crack would then lead to a similar tensile crack forming at the top of the slab at the point of maximum hogging moment. Consideration of the geometric shape of the failure surfaces and the rotation required at each crack allows the ultimate moment at failure to be determined.

Concrete Society Technical Report 34 Equations

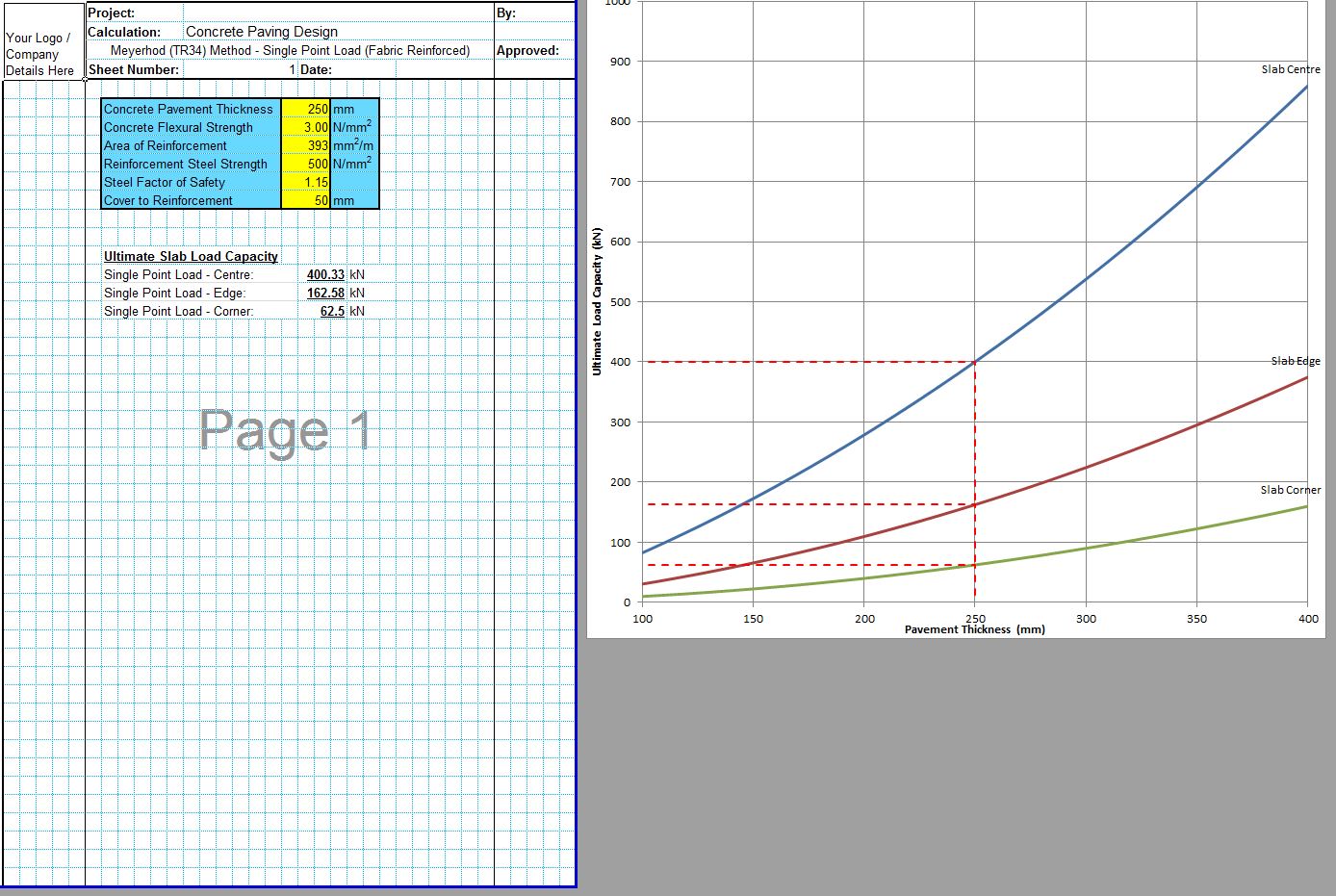
The Meyerhof equations are presented below where P_u is the ultimate load capacity of the slab, M_p is the ultimate sagging moment and M_n is the ultimate hogging moment. For multiple loadings x and y are the spacing between the loads in the x and y directions, and l is the radius of relative stiffness. For patch loadings a is the effective radius of the patch load.

For multiple loadings it should be considered that generally if the loads are spaced further apart than the radius of relative stiffness of the slab, the multiple load cases may not be the critical condition for slab design. In this case the single load case should be checked to see which condition is critical.

To determine the maximum hogging and sagging moments which can be accommodated by a plain concrete slab the below equation can be used where f_ctd,fl is the characteristic flexural strength of the concrete and h is the slab thickness. Further information on determining the flexural strength of the concrete is given in our Flexural Strength of Concrete post. Flexural strength estimation tools are also included with the full CivilWeb Rigid Pavement Design Suite.

A concrete slab with a layer of structural reinforcement fabric at the bottom of the slab can be determined using the below equation where A_s is the area of steel reinforcement per m, f_yk is the characteristic strength of the reinforcement steel, d is the effective depth and γ_m is the steel material factor of safety (typically taken as 1.15).

Note that any structural reinforcement at the top of the slab for crack control is not included in this equation. Where only top reinforcement is present the plain concrete equation should be used. Also note that the onset of cracking in the concrete is not affected by any steel reinforcement, the steel simply helps to hold the cracked concrete together. So where the design limit is at the onset of cracking, the plain concrete equation should be used even if some reinforcement is included.

Concrete Society Technical Report 34 - Point Load Equations

Concrete Society Technical Report 34- Four Point

Concrete Society Technical Report 34 - Patch Load Equations

For the patch load equations to be suitable the value of the patch area radius (a) divided by the radius of relative stiffness (l) should be greater than 0.2. If the value is less than 0.2, the maximum load can be determined by interpolating between the point load equation results and the patch load equation results.

Concrete Society Technical Report 34- Modes of Failure

Assumptions & Limitations with Concrete Society Technical Report 34

The Concrete Society Technical Report 34 method suffers from many of the same limitations as the Westergaard method. Again this method does not account for environmentally induced stresses in the pavement from warping, curling and thermal expansion.

The Meyerhof limit state design approach is well suited to floors subjected to large static loads from racking or mezzanine floors for example. In these cases failure of the concrete slab would be total collapse rather than the effects of fatigue induced from millions of wheel loads. Also internal floor slabs are less prone to environmental damage and effects.

Concrete Society Technical Report 34 is intended for the design of internal warehouse floors and as such is well suited to the Meyerhof limit state method.

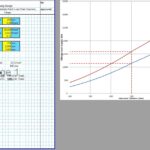
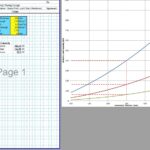
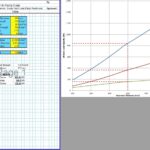
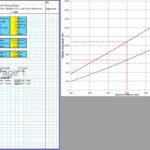
CivilWeb Concrete Society Technical Report 34 Concrete Pavement Design Spreadsheet

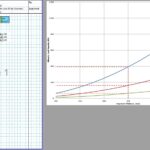
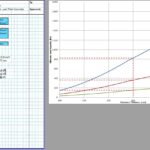
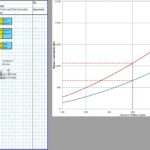
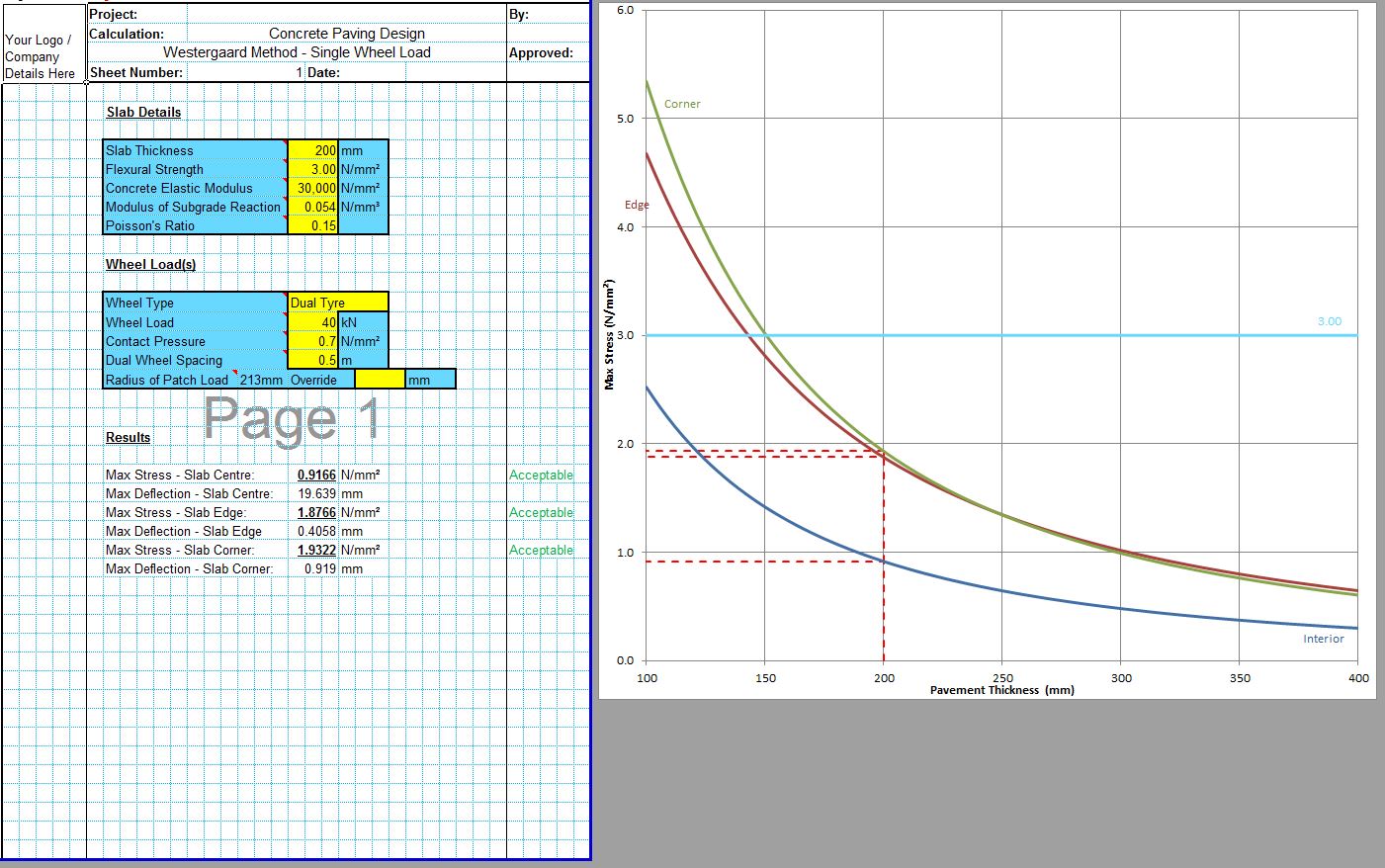
The CivilWeb Concrete Society Technical Report 34 Concrete Pavement Design Spreadsheet allows the designer to design a compliant concrete pavement design within seconds with only a handful of inputs. Our unique design tools also allow the designer to optimise the design in moments, with the optimum design thickness shown on a graph.

The CivilWeb Concrete Society Technical Report 34 Concrete Pavement Design spreadsheet includes modules for designing concrete pavement slabs subjected to single point, single patch, double point, double patch or quadruple point or patch loads. These can be designed for either plain concrete pavements or slabs containing fabric reinforcement.